The diagonals of a parallelogram divide it into four triangles of equal area. Consecutive angles are supplementary A D 180.

The Diagonals Of A Parallelogram Bisect Each Other Geometry Help

To answer this question we must find the diagonal of a rectangle that is by Because a rectangle is made up of right angles the diagonal of a rectangle creates a right triangle with two of the sides.

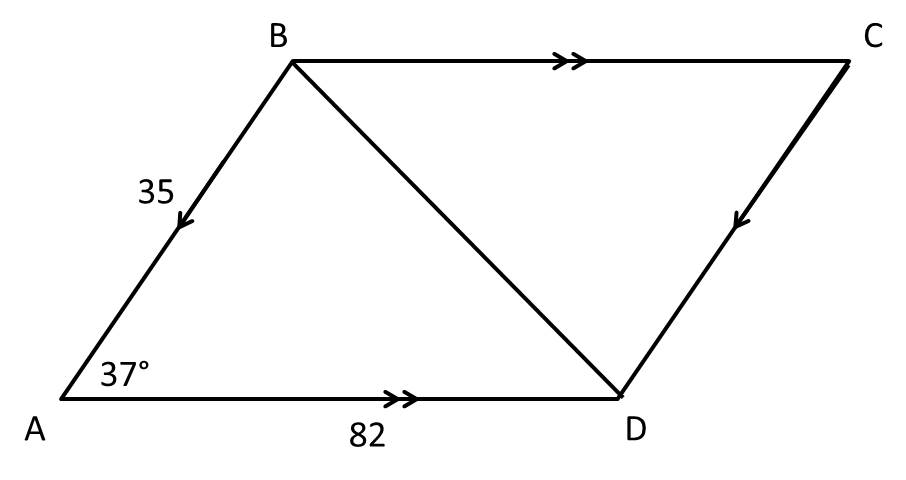
Diagonals of a parallelogram. Diagonals of a parallelogram The use of vectors is very well illustrated by the following rather famous proof that the diagonals of a parallelogram mutually bisect one another. In other words the diagonals intersect each other at the half-way point. And what I want to prove is that its diagonals bisect each other.

These are lines that are intersecting parallel lines. What are the diagonals of a parallelogram. To explore these rules governing the diagonals of a parallelogram use Math Warehouses interactive parallelogram.

Opposite angels are congruent D B. Try this Drag the orange dots on each vertex to reshape the parallelogram. Because the parallelogram has adjacent angles as acute and obtuse the diagonals split the figure into 2 pairs of congruent triangles.

So the first thing that we can think about-- these arent just diagonals. The diagonals bisect each other. The diagonals bisect each other.

Where pq are the diagonals. Ex 81 2 If the diagonals of a parallelogram are equal then show that it is a rectangle. So if opposite sides of a quadrilateral are parallel then the quadrilateral is a parallelogram.

Proving that a quadrilateral is a parallelogram if and only if its diagonals bisect each otherWatch the next lesson. The diagonals of a parallelogram are equal true or false. 3 Show answers.

Further formulas are specific to parallelograms. Ab are the parallel sides. The diagonals of a parallelogram bisect each other.

Let ABCD be a parallelogram where AC BD To prove. If one angle is right then all angles are right. A parallelogram Suppose that the quadrilateral ABCD in Fig.

The diagonals bisect each other. AO OD CO OB. A parallelogram is a quadrilateral that has opposite sides that are parallel.

So you can also view them as transversals. The diagonals of a parallelogram bisect each other. Ifigured out the question and i dont know what to put here.

All of the area formulas for general convex quadrilaterals apply to parallelograms. Opposite sides are congruent AB DC. There are six important properties of parallelograms to know.

The diagonals of a parallelogram are not equal. A parallelogram has two pairs of equal sides. The diagonals of a parallelogram bisect each other.

That is each diagonal cuts the other into two equal parts. 13 is a parallelogram. So we have a parallelogram right over here.

A parallelogram can be rearranged into a rectangle with the same area. In any parallelogram the diagonals lines linking opposite corners bisect each other. If you just look at a parallelogram the things that look true namely the things on this list are true and are thus properties and the things that dont look like theyre true arent properties.

Since the angles are acute or obtuse two of the shorter sides of the triangles both acute and obtuse are congruent. Diagonals of a parallelogram are the segments which connect the opposite corners of the figure. Diagonals of a parallelogram if you know area angle between the diagonals and other diagonal.

Diagonals of a Parallelogram The diagonals of a parallelogram bisect each other. One pair of opposite sides is parallel and equal in length. It has two pairs of equal angles.

Another question on Mathematics. Notice the behavior of the two diagonals. Parallelograms have opposite interior angles that are congruent and the diagonals of a parallelogram bisect each other.

The opposite sides are parallel. Diagonals of a parallelogram if you know sides and angle or sides and other diagonal- smaller diagonal- larger.

Its diagonals bisect with each other. AC and OB are diagonals In the figure let the intersecting point of OB and AC be P To show that diagonals bisect each other we have to prove that OP PB and PA PC The co-ordinates of P is obtained by.

Proof Rectangle Diagonals Bisect Each Other Youtube

Comparison of properties of each type of parallelogram Criteria prove quadrilateral is a parallelogram Menu.

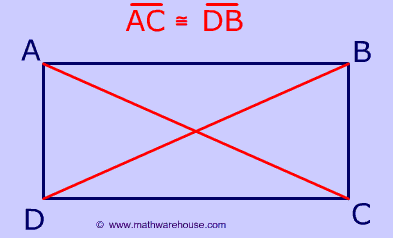
Diagonals of a rectangle bisect each other. The diagonals meet at right angles. The diagonals lines linking opposite corners bisecteach other at right angles 90. OP OB.

The diagonals bisect each other. One of the diagonals bisects the other. It is possible only for square.

That is each diagonal cuts the other into two equal parts and the angle where they cross is always 90 degrees. Answers Igot 108 hope thats right. The opposite sides are parallel.

The sum of the squares of the sides equals the sum of the squares of the diagonals. Prove that diagonals of a rectangle bisect each other and are equalcoordinatebyktcFor Short Notes Revision Notes And NCERT SolutionVisit Us at- wwwkw. If in a parallelogram its diagonals bisect each other right angle and are equal then it is a aSquare bRectangle cRhombus dKite.

Is a rectangle is a parallelogram. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. The diagonals bisect each other.

How do you prove that rectangle diagonals bisect each other. Adjacent angles are supplementary. Opposite angles are congruentC.

In todays video we will be going over the simple geometry proof that the diagonals of a rectang. No diagonal of rectangle does not bisect each other at right angles. Since the diagonals bisect each other y 16 and x 22.

It is only possible when adjacent sides of rectangle are equal. One pair of opposite sides is parallel and equal in length. Some trapeziums have one line of symmetry.

Vertexto reshape the rhombus and convince your self this is so. Click to see full answer. Diagonals bisect the angles D.

We can prove it by using congruencyWe have to prove that the adjacent triangles in rectangle are congruent. Diagonals bisect each otherB. The length of the mid-segment is equal to 12 the sum of the bases.

Diagonals bisect each other. A rectangle has two pairs of equal sides. A diagonal of a rectangle is inclined to one side of the rectangle at 2 5 o.

Similarly we can prove that PC PA. Which of the following is NOT true regarding a rectangle. Yes since opposite angles are congruent.

Thus a rectangle has all the properties of a parallelogram. A rectangle is a quadrilateral with four right angles. The diagonals of a rectangle bisects each other.

Thus diagonals bisect each other in a rectangle. Each diagonal divides the quadrilateral into two congruent triangles. It has four right angles 90.

Two angles on the same side are supplementary that is the sum of the angles of two adjacent sides is equal to 180. The acute angle between the diagonals is. The acute angle between the diagonals is.

Which statement can be used to prove that a given parallelogram is a rectangleThe opposite angles of the parallelogram are congruentThe consecutive sides of the parallelogram are congruentThe diagonals of the parallelogram bisect each otherThe diagonals of the parallelogram are congruent. A trapezium has one pair of parallel sides. Solution for Properties of Quadrilaterals Diagonals Diagonals Diagonals Diagonals Exactly bisect each other Base Opposite Opposite sldes All angles congruent.

Since the legs of an isosceles trapezoid are congruent and the following pairs of triangles share a base ABD DCA and ABC DCB by the Side-Side-Side postulate. It has two adjacent angles that are supplementary that is they add up to 180 degrees.

Prove That The Diagonals Of A Trapezium Divide Each Other Proportionally Youtube

The diagonal of the trapezoid connects from either bottom angle of the trapezoid to the far upper corner of the rectangle.

Diagonals of a trapezoid. The number of sides in trapezoid is four. Quadrilaterals Trapezoid This investigation is about discovering the relationships sides angles and the diagonals of the isosceles trapezoid. It has a pair of parallel sides.

Properties of a Trapezium Like other quadrilaterals the sum of all the four angles of the trapezium is equal to 360. Calculate the area of the trapezoid. Where is the point between and representing the base of the triangle.

Let ABCD be a trapezoid. 1 Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition or because it has no line of symmetry. The height of a trapezoid is 10 cm.

The bases top and bottom of an isosceles trapezoid are parallel. A Trapezium has two parallel sides and two non-parallel sides. Through diagonals and angle between them The area of a trapezoid across the diagonals and the angle between them is considered the conditional division of the trapezoid into four triangles just like the area of any arbitrary quadrangle.

So I dont know what I did wrong. Assume temporarily that the diagonals of the trapezoid bisect each other that is. Opposite sides of an isosceles trapezoid are the same length congruent.

The angles on either side of the bases are the same sizemeasure congruent. Diagonal of an isosceles trapezoid is the line segment joining two non-adjacent vertices of the trapezoid and is represented as dsqrt abc2 or Diagonalsqrt Side ASide BSide C2. If a quadrilateral is known to be a trapezoid it is not.

495 1121 Views. The diagonals not show here are congruent. On the homework I solved this using D1D2 2 and my teacher marked me wrong.

The number of angles in trapezoid is four. The only trapezoid that has congruent diagonals is the isosceles trapezoid. This diagonal connects to form another right triangle where the sum of the solved triangular base and the rectangle length is a leg and the altitude of the trapezoid is another leg.

Properties of the sides of an isosceles trapezoid. Become a member and. The two diagonals of an isosceles trapezoid are congruent.

Angle BAE angle DCE and angle ABD angle CDE. The diagonals not show here are congruent. The formula for the length of diagonal uses the Pythagoreon Theorem.

Construct point E as the intersection of the diagonals AC and BD. Trapezoid has two diagonals and both bisect each other. Given a convex quadrilateral the following properties are equivalent and each implies that the quadrilateral is a trapezoid.

The angle between a side and a diagonal is equal to the angle between the opposite. Its diagonals bisect with each other. Therefore Δ s A O B and D O C are congruent by the SAS axiom.

The bases are parallel by definition. A Trapezium has 4 unequal sides. They also form congruent triangles.

The lengths of the two diagonals of the trapezoid are 30 cm and 50 cm. By the diagonals are transversals so the marked angles are equal. Adding these two values together we get.

26 Votes A trapezium or a trapezoid is a quadrilateral with a pair of parallel sides. Because of the way the dimensions are the same the diagonals are of equal. See full answer below.

The following figure shows a trapezoid to the left and an isosceles trapezoid on the right. Plugging in our values we get. Then the corresponding parts A B and D C of these congruent triangles will be congruent.

Dividing by two we have the length of each additional side on the bottom of the trapezoid. The properties of the trapezoid are as follows. In the isosceles trapezoid below diagonals AC and BD are congruent.

Two angles on the same side are supplementary that is the sum of the angles of two adjacent sides is equal to 180. Thus by AA the triangles ABE and CDE are similar. A O O C and D O O B.

Diagonals The defining trait of this special type of trapezoid is that the two non-parallel sides XW and YZ below are congruent. The diagonals of trapezium bisect each other. A trapezoid is a quadrilateral with exactly one pair of parallel sides the parallel sides are called bases.

The length of the mid-segment is equal to 12 the sum of the bases.

Yes since opposite sides are congruent. Prove by vector method that the quadrilateral whose diagonal bisect each other is a parallelogram.

Proof Diagonals Of A Parallelogram Bisect Each Other Hindi Video Khan Academy

Two angles on the same side are supplementary that is the sum of the angles of two adjacent sides is equal to 180.

Diagonals bisect each other. Its diagonals bisect with each other. The Diagonals of a Square Bisect Each Other Problem. AO OD CO OB.

The opposite sides are parallel. ABCD is a parallelogram diagonals AC and BD intersect at O In triangles AOD and COB DAO BCO alternate interior angles. Also show that they bisect each other at right angles.

A trapezium or a trapezoid is a quadrilateral with a pair of parallel sides. Click to see full answer. Notice the behavior of the two diagonals.

Prove using vectors two lines bisect each other. The length of the mid-segment is equal to 12 the sum of the bases. Thus diagonals bisect each other in a rectangle.

The diagonals bisect each other. Since the diagonals bisect each other y 16 and x 22. Proving that a quadrilateral is a parallelogram if and only if its diagonals bisect each otherWatch the next lesson.

The four small triangles are congruent by SSS. Is a rhombus a parallelogram. Two angles on the same side are supplementary that is the sum of the angles of two adjacent sides is equal to 180.

The diagonals of a parallelogram bisect each other. This means the diagonals form four angles that are congruent and must measure 90 degrees each. The diagonals of a rectangle bisects each other and equal.

Each diagonal divides the quadrilateral into two congruent triangles. If in a parallelogram its diagonals bisect each other right angle and are equal then it is a aSquare bRectangle cRhombus dKite. Show that its diagonals bisect each other that is prove that AOOC and BOOD.

Its diagonals bisect with each other. To explore these rules governing the diagonals of a parallelogram use Math. Adjacent angles are supplementary.

A trapezium or a trapezoid is a quadrilateral with a pair of parallel sides. Diagonals bisect each other. Httpsbitly3akrBoz to get all learning resources as per ICSE CBSE IB Cambridge.

Show Answer x 40 2x 18 40 x 18 40 x 18 22 x. A rhombus has four sides of equal lengths. When we attempt to prove that the diagonals of a square bisect each other we will use congruent triangles.

Solution for Properties of Quadrilaterals Diagonals Diagonals Diagonals Diagonals Exactly bisect each other Base Opposite Opposite sldes All angles congruent. The length of the mid-segment is equal to 12 the sum of the bases. The diagonals of a parallelogram bisect each other.

Theorem 87 If the diagonals of a quadrilateral bisect each other then it is a parallelogram. Trapezoid has two diagonals and both bisect each other. The diagonals bisect each other.

Prove by vector method that the diagonals of a rhombus bisect each other. In any parallelogram the diagonals lines linking opposite corners bisect each other. It has two pairs of equal angles.

Try this Drag the orange dots on each vertex to reshape the parallelogram. What is x and Y. One pair of opposite sides is parallel and equal in length.

Rhombus Square 32 Rhombus Note. ABCD is a square. That is each diagonal cuts the other into two equal parts.

Proof that the diagonals of a. The diagonals bisect each other at right.