By following these steps. This moves the asymptote to the line y3.

Math Scene Functions 2 Lesson 3 Rational Functions And Asymptotes

Remember that the equation of a.

Equation of the asymptote. Has a curvilinear asymptote y x 2 2x 3 which is known as a parabolic asymptote because it is a parabola rather than a straight line. F x 3 is a translation of that graph by 3 units in the positive y directive ie. In general you can skip the multiplication sign so 5x is equivalent to 5x.

The graph has a vertical asymptote with the equation x 1. What is the equation of horizontal asymptote. Use the slope from Step 1 and the center of the hyperbola as the point to find the pointslope form of the equation.

Fx -X2 16 x2 5x 4 y -1 y 0 no horizontal asymptotes O y-16 Use the graph to find the horizontal asymptote if any of the function. The calculator can find horizontal vertical and slant asymptotes. 10 -10 10 x - 10 y -4 y 4 x -4 x 4 y 1 y 0 y 1 O O y 1 Find the domain of the rational function.

Finding All Asymptotes of a Rational Function Vertical Horizontal. Lim_xrightarrow a-0fxpm infty or lim_xrightarrow a0fxpm infty. An exponential function is just one of the types of functions.

You can use this method to find any nonlinear asymptote on the TI-89. Hence the equation of the oblique asymptote is boldsymboly -2x 10. An asymptote is a line that a curve approaches as it heads towards infinity.

Give an example of a rational function that has vertical asymptote x 3 and x -3 horizontal asymptote y 2 and y-intercept is 0 4 Math. Give the equation of the horizontal asymptote if any of the function. Asymptotes and curve sketching.

Click the blue arrow to submit and see the result. The asymptote calculator takes a function and calculates all asymptotes and also graphs the function. This means that the quotient of boldsymbolpx and boldsymbolqx is equal to boldsymbol-2x 10.

The calculator will find the vertical horizontal and slant asymptotes of the function with steps shown. Solve for y to find the equation in slope-intercept form. An asymptote of a curve y f x that has an infinite branch is called a line such that the distance between the point xf x lying on the curve and the line approaches zero as the point moves along the branch to infinity.

For the original function f x1x the asymptote is the x-axis or y0. Vertical asymptotes can be found by solving the equation nx 0 where nx is the denominator of the function note. To find the vertical asymptote we solve the equation x 1 0 x 1.

Enter the function you want to find the asymptotes for into the editor. To find the horizontal asymptote we calculate. The direction can also be negative.

The quadratic function y x 2 2x 11 is the equation of the nonlinear asymptote. The graph has a vertical asymptote with the equation x 1. This only applies if the numerator tx is not zero for the same x value.

Asymptote Equation We know that the vertical asymptote has a straight line equation is x a for the graph function y fx if it satisfies at least one the following conditions. Vertical asymptote at x5 horizontal asymptote at y-3 and x-intercept is 52. You have to do each asymptote.

Asymptotes can be vertical oblique slant and horizontal. Horizontal vertical and oblique. There are three types.

Find the slope of the asymptotes. Learn how to find the verticalhorizontal asymptotes of a function. State an equation of a rational function that satisfies the given conditions.

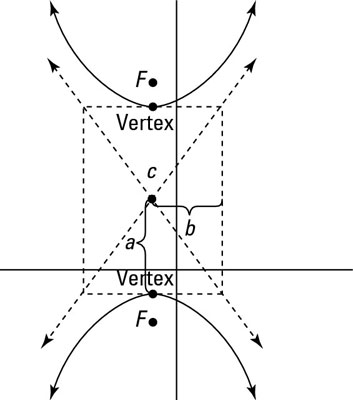
Find the asymptotes for the function. Divide both sides of the equation by 144 to get 1 on the right hand the equation will be x29 y216 1 a3 and b4 so the equation of asymptote will be y - ba x and y ba x so y - 43x and y 43x. Recall that the quotient of dfracpxqx will return the equation for the functions oblique asymptote.

The curve can approach from any side such as from above or below for a horizontal asymptote. How do you find all Asymptotes. This type of function is mostly used in simulating the growth or.

Find the asymptotes for the function. The numerator always takes the value 1 so the bigger x gets the smaller the fraction becomes. An asymptote is a line that the graph of a function approaches but never touches.

Asymptotes are used in procedures of curve sketching. An asymptote serves as a guide line to show the behavior of the curve towards infinity.