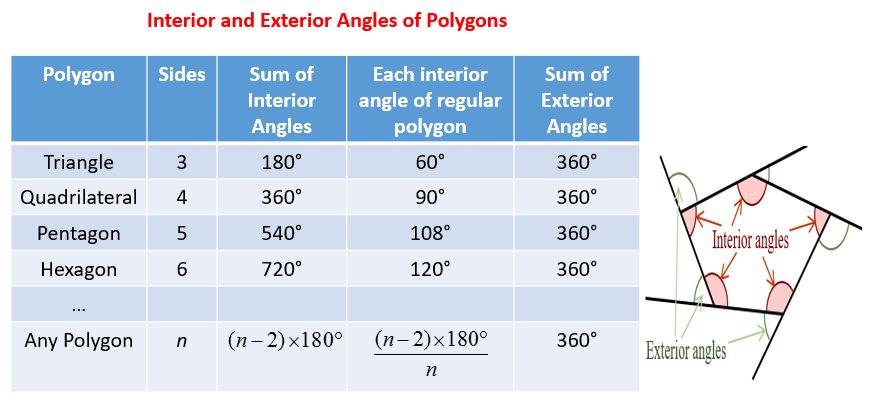
In general a regular polygon has exterior angles of 360 N degrees if it has N sides. 360 formula to find the number of sides of a regular polygon when the measure of each exterior angle is known.
How Is The Formula For Exterior Angles Of A Polygon Determined Quora
The sum of the exterior angles of a regular polygon will always equal 360 degrees.
Formula for exterior angle of a regular polygon. All the Exterior Angles of a polygon add up to 360 so. Sum of Interior angles of Polygon IA n-2 x 180. Therefore the number of sides 360 36 10 sides.
Interior and exterior angle formulas. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. The formula for calculating the size of an exterior angle is.
We can get the equation of interior angles from this. In any polygon the sum of exterior angles is 36 0 Formula to find the measure of each exterior angle of a regular n-sided polygon is. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.
Interior angle Exterior angle 180 Exterior angle 180-144 Therefore the exterior angle is 36 The formula to find the number of sides of a regular polygon is as follows. Correct answer to the question. In any polygon the sum of an interior angle and its corresponding exterior angle is.
The sum of the measures of all the exterior angles of a polygon is 360. The sum of the exterior angles of a polygon is 360. Exterior angle of a polygon 360 number of sides.
360 n. Exterior angle of regular polygon is given by frac 360 0 n where n is number of sides of a regular polygon. For any given regular polygon to find the each exterior angle we have a formula.
How to calculate Measure of exterior angle of regular polygon. Interior angle corresponding exterior angle 1800 The sum of the measures of the interior angles of a polygon with n sides is given by the general formula n2180. Angles of a Regular Polygon.
The formula to working out the exterior angle of a polygon is this. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o. There are as many exterior angles as there are sides n and they are all equal.
Interior angle 180 - 360N. Each exterior angle must be 360n where n is the number of sides Press play button to see. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides.
The sum of exterior angles of a polygon is 360. For example the interior angles of a pentagon always add up to 540 no matter if it regular or irregular convex or concave or what size and shape it is. Hence the polygon has 10 sides.
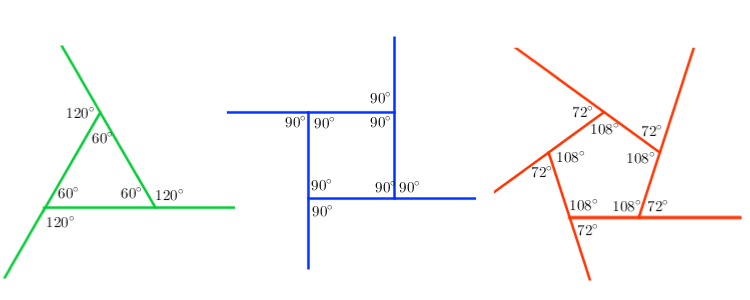
For a square the exterior angle is 90 90. Since you are extending a side of the polygon that exterior angle must necessarily be supplementary to the polygons interior angle. Using our new formula any angle n 2 180 n For a triangle 3 sides 3 2 180 3 1 180 3 180 3 60.
The sum is divided by n to find each exterior angle. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360. Since each exterior angle is equal that means each exterior angle is 360 6 60 degrees.
In this formula n is the number of sides of the polygon. The number of Sides is used to classify the polygons. Then we have 36 0 9 4 0 Hence the measure of each exterior angle of a regular polygon is 4 0.
By using this formula easily we can find the exterior angle of regular polygon. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Number of Sides of a Regular Polygon 360 Magnitude of each exterior angle.
Download PDF for free. Formula for exterior angle of regular polygon as follows. Together the adjacent interior and exterior angles will add to 180 180.
To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. 360 divided number of sides So lets use this formula to work out the answer.
So our new formula for finding the measure of an angle in a regular polygon is consistent with the rules for angles of triangles that we have known from past lessons. For our equilateral triangle the exterior angle of any vertex is 120 120. Calculating the size of each exterior angle of regular polygons The formula for calculating the size of an exterior angle of a regular polygon is.
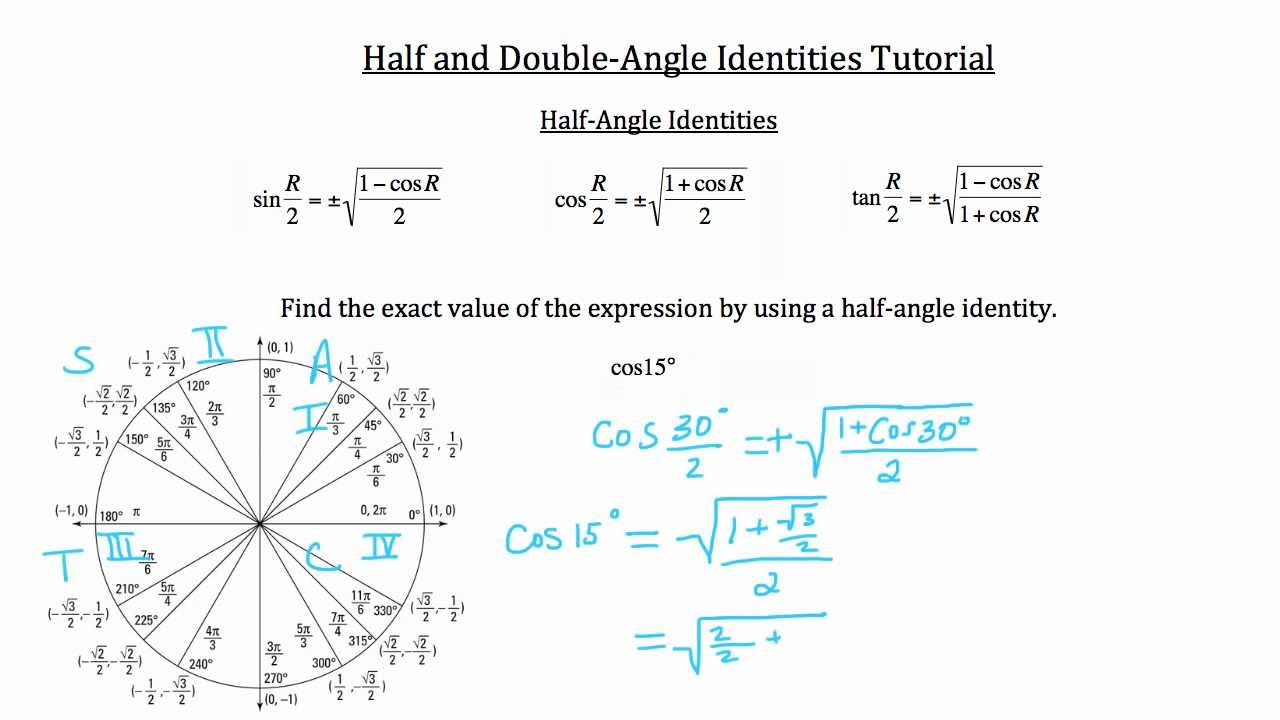
The halfangle identities for the sine and cosine are derived from two of the cosine identities described earlier. C o s a 2 1 c o s a 2.
Half Angle And Double Angle Identities Youtube
The common trigonometry angles are 0 30 45 60 and 90.
Half angle trig identities examples. If the angle lies in the first quadrant then all positive means sine half angle identity will be positive. You da real mvps. So we need to verify.
We obtain half-angle formulas from double angle formulas. Plot of the six trigonometric functions the unit circle and a line for the angle θ 07 radians. Thanks to all of you who support me on Patreon.
Definition of the Trig Functions Right triangle definition For this definition we assume that. First note that which falls from the identity. You can continue to halve any angle on the unit circle for the rest of your life if you have nothing better to do and take the trig functions of those angles.
For example using these formulas we can transform an expression with exponents to one without exponents but whose angles are multiples of the original angle. For example to solve for the trigonometric functions. 53 Half-Angle Formulas At times is it important to know the value of the trigonometric functions for half-angles.
But also we may have a formula for half-angle values which are commonly used. Half Angle Identities to E. This branch of mathematics divides into two sub-branches called plane trigonometry and spherical geometry.
In this section you will learn formulas that establish a relationship between the basic trigonometric values sin cos tan for a particular angle and the trigonometric values for an angle that is either double- or half- of the first angle. If we replace θ with α 2the half-angle formula for sine is found by simplifying the equation and solving for sinα 2. Trigonometric Double-Angle and Half-Angle Formulas Written by tutor Michael B.
S i n a 2 1 c o s a 2. Half Angle Formula Cosine Simply by using a similar process With the same substitutions we did above. The formula for half angle identities is as below.
1 per month helps. Example 1 Find the exact value of the expression sin 120 degrees by using the half angle formula STep by step video. If α2 is in the first or second quadrants the formula uses the positive case.
Use the Half-Angle formulas to find Answer. Find the exact value for sin 105 using the halfangle identity. Then Using the above formulas we get Since then is a positive number.
Solving gives us the following sine of a half-angle identity. The next set of identities is the set of half-angle formulas which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. Sinθ Tanθ and 1 are the heights to the line starting from the x-axis while Cosθ 1 and Cotθ are lengths along the x-axis starting from the origin.
A half-angle identity can be used to calculate the trigonometric functions if the trigonometric function of double the given angle is known. Also called half number identities half angle identities are trig identities that show how to find the sine cosine or tangent of half a given angle. Verify the identity AnswerWe have Using the Double-Angle formulas we get Putting stuff together we get From the Double-Angle formulas one may generate easily the Half-Angle formulas In particular we have Example.
The points labelled 1 Secθ Cscθ represent the length of the line segment from the origin to that point. The half-angle formulas for sine cosine and tangent are as follows. On the right side cos 2θ becomes cos θ because 2 12 1.
Both sin 2A and cos 2A are obtained from the double angle formula for the cosine. Sine of a Half Angle. And if it is in 3rd or 4th quadrant we will introduce a negative sign with the sine half angle identity.
Instead of using a sum or difference formula we can now say that 15 degrees is half of 30 degrees which is an angle on the Unit Circle. Various formulas are there to use these angles and provide sides easily. Therefore we have Same arguments lead to Example.
With half angle identities on the left side this yields after a square root cos θ2 or sin θ2. For example 15 degrees is half of 30 degrees and 75 degrees is half of 15 degrees. The sign of the two preceding functions depends on the quadrant in which the resulting angle is located.
Double Angle Formulas 22 2 2 2 sin22sincos cos2cossin 2cos1 12sin 2tan. If x is an angle in degrees and t is an angle in radians then 180 and 180180 txt tx x pp p Þ Half Angle Formulas alternate form 2 2 2. For a problem like sin π12 remember that θ2 π12 or θ π6 when substituting into the identity.
Cosine of a Half Angle. Check the identities Answer. Sin alpha2-sqrt1-cos alpha2 The sign positive or negative of sinalpha2 depends on the quadrant in which α2 lies.
The Corbettmaths video tutorial on Angles in Polygons. The sum of the measures of the interior angles of a polygon with n sides is n 2180.
Sum Of Interior Exterior Angles Polygons Pentagon Tutors Com
Calculate the exterior angles of the irregular pentagon below.
Exterior angle of a pentagon. Example 1 - Regular pentagon. A pentagon has 5 interior angles so it has 5 interior-exterior angle pairs. 3 Show answers Another question on Mathematics.
Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side. If the side of a polygon is extended the angle formed outside the polygon is the exterior angle. Together the adjacent interior and exterior angles will add to 180 180.
The exterior angles of a rectangle are each 90. The diagonals bisect each other. The exterior angle is 360 5 72.
The marked angles are called the exterior angles of the pentagon. The measure of each interior angle of an equiangular n -gon is. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides is calculated using Measure of exterior angle 360Number of sides.
The measure of each interior angle is and the measure of each exterior angle is. The opposite sides are parallel. Feel free to move the vertices of these polygons anywhere youd like.
The Exterior Angles of a Polygon add up to 360. To find the sum of the interior angles you multiply 3 by 180. Interior and exterior angles formed within a pair of adjacent sides form a complete 180 degrees angle.
The exterior angles of a triangle quadrilateral and pentagon are shown respectively in the applets below. The interior angle is 180 72 108. The sum of the exterior angles of a polygon is 360.
The exterior and interior angles add up to 180 notice the line they sit on in the diagram. The pentagon 5-sided shape above can be split into 3 triangles. A regular pentagon has the following properties.
Check here for more practice. For our equilateral triangle the exterior angle of any vertex is 120 120. Interior angle sum of a pentagon.
Since you are extending a side of the polygon that exterior angle must necessarily be supplementary to the polygons interior angle. With our tool you need to enter the respective value for Number of sides and hit the calculate button. But the exterior angles sum to 360.
When we add up the Interior Angle and Exterior Angle we get a straight line 180. You can control the size of a colored exterior angle by using the slider with matching color. An exterior angle basically is formed by the intersection of any of the sides of a polygon and extension of the adjacent side of the chosen side.
Find the measure of each interior angle and each exterior angle of a regular pentagon. Measures of Exterior Angles They are formed on the outer part that is the exterior of the angle. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o.
The sum of the exterior angles of a polygon is 360. Exterior angles of polygons. Exterior angles of polygons.
To calculate Measure of exterior angle of regular polygon you need Number of sides n. A Polygon is any flat shape with straight sides. For a square the exterior angle is 90 90.
Interior angles that measure 108 Exterior angles that measure 72 A regular pentagon has an area of approximately 17204774 s2 where s is equal to the side length. When any internal angle is greater than 180 it is concave. Concave or Convex A convex pentagon has no angles pointing inwards.
They are Supplementary Angles. More precisely no internal angles can be more than 180. Which of the expressions on the photo document i inserted together represent all.
Videos worksheets 5-a-day and much more. If the side of a polygon is extended the angle formed outside the polygon is the exterior angle. Each exterior angle is paired with a corresponding interior angle and each of these pairs sums to 180 they are supplementary.
It has four right angles 90. These pairs total 5180900. If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.
The interior and exterior angles add up to 180 The exterior angle is 180 - 108 72 Question.
The number of sides of the polygon. The formula for calculating the size of an interior angle is.
Q28 Answers Paper 1 November 18 Edexcel Gcse Maths Foundation Elevise
To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.
Each exterior angle of a regular polygon. Check here for more practice. A Calculate the size of each interior angle in the regular polygon. The sum of the measures of the interior angles of a polygon with n sides is n 2180.
Each exterior angle must be 360n where n is the number of sides Press play button to see. All the Exterior Angles of a polygon add up to 360 so. The other side ac is split into lengths of x and x 12.
1 Show answers Another question on Mathematics. The measure of maximum possible exterior angle in a regular polygon is. The answer is 180 72 108.
What is the length of ac. An exterior angle basically is formed by the intersection of any of the sides of a polygon and extension of the adjacent side of the chosen side. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Correct answer to the question if a regular polygon has exterior angles that measure 40 degrees each how many sides does the polygon have. The measure of each interior anglec. Find the measure of each exterior angle of regular polygons with sides 4 0.
Interior angle of a polygon sum of interior angles number of sides. Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. The measure of each exterior angleb.
Ex 32 5 a Is it possible to have a regular polygon with measure of each exterior angle as 22Given that Exterior angle 22 Let number of sides n In a regular Polygon Sum of the exterior angles 360 22 n 360 n 360 22 n 1636 Since n cannot be in decimals 22 external angle is not possible Ex 32 5 b Can it be an interior angle of a regular polygon. All the interior angles in a regular polygon are equal. To find the sum of its interior angles substitute n 5 into the formula 180n 2 and get 1805 2 1803 540 Since the pentagon is a regular pentagon the measure of each interior angle will be the same.
Which is the same as the number of sides. Measures of Exterior Angles They are formed on the outer part that is the exterior of the angle. Find the number of sides of a regular polygon if each exterior angle measures.
Aline parallel to a triangles side splits ab into lengths of x - 5 and x 2. We do this by subtracting the exterior angle of 72 from 180. Solution for Find the measure of each exterior angle of a regular polygon whose central angle measures a 45.
The sum of the exterior angles of a polygon is 360. The ratio between the exterior and interior angle of a regular polygon is 15 finda. To find the size of each angle divide the sum 540º by the number of angles in the pentagon.
The sum of the measures of the exterior angles of a convex polygon one angle at each vertex is 360 The measure of each exterior angle of a regular n-gon is 360 n. How many sides does a regular polygon have if each exterior angle has a measure of 15. 360 div number of sides.
Interior and exterior angles formed within a pair of adjacent sides form a complete 180 degrees angle. The sum of the exterior angles of a regular polygon will always equal 360 degrees. 540 5 108 There are 108 in each interior angle of a regular pentagon.
For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360. Correct answer to the question.
The formula for calculating the size of an exterior angle in a regular polygon is. A regular polygon has equal exterior angles of 72.
